this post was submitted on 19 Sep 2024
366 points (92.2% liked)
Funny: Home of the Haha
5700 readers
1548 users here now
Welcome to /c/funny, a place for all your humorous and amusing content.
Looking for mods! Send an application to Stamets!
Our Rules:
-
Keep it civil. We're all people here. Be respectful to one another.
-
No sexism, racism, homophobia, transphobia or any other flavor of bigotry. I should not need to explain this one.
-
Try not to repost anything posted within the past month. Beyond that, go for it. Not everyone is on every site all the time.
Other Communities:
-
/c/TenForward@lemmy.world - Star Trek chat, memes and shitposts
-
/c/Memes@lemmy.world - General memes
founded 1 year ago
MODERATORS
you are viewing a single comment's thread
view the rest of the comments
view the rest of the comments
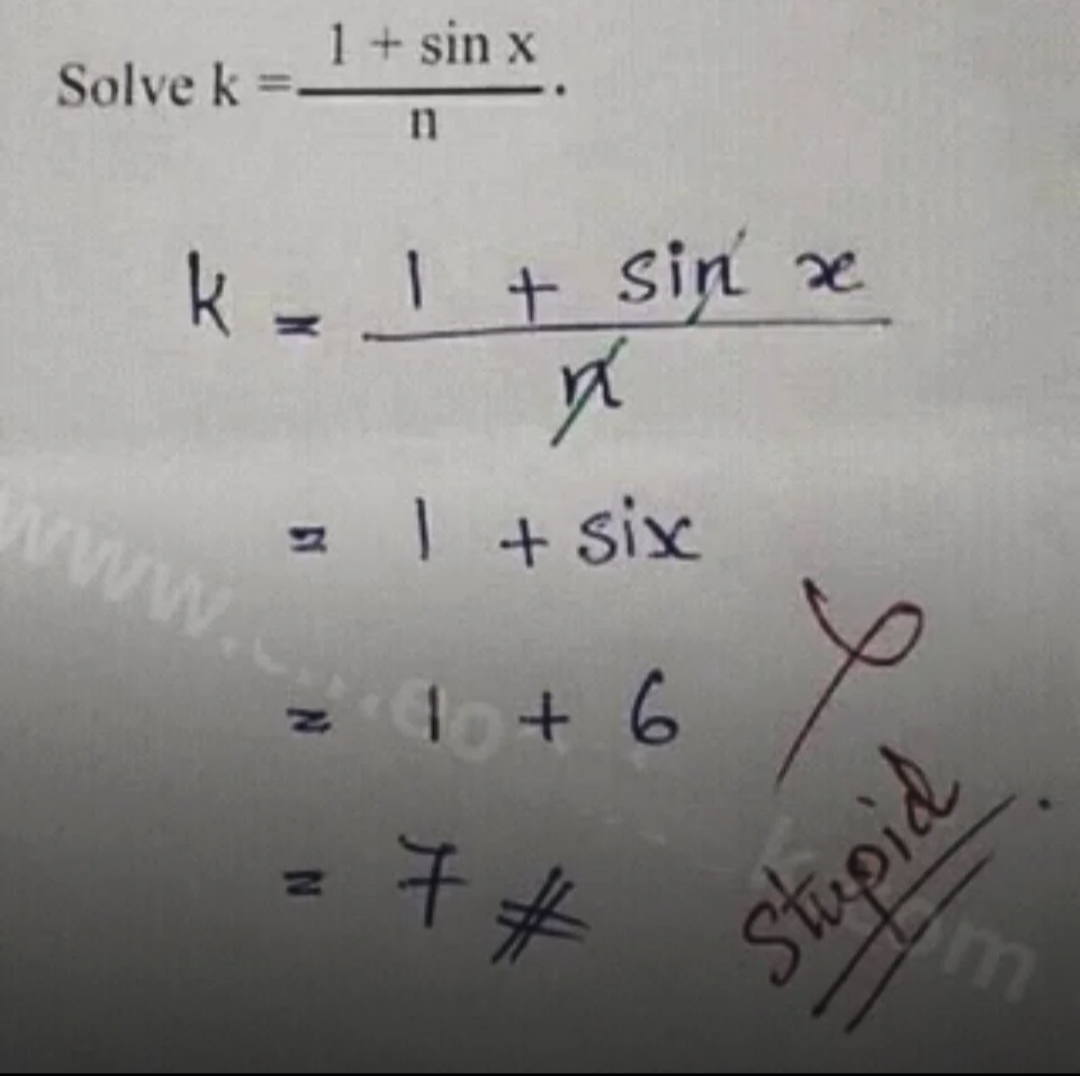
There's 3 variables and 1 equation. This is unsolvable.
Since we're just making shit up anyway
Assume k=0 and n is the last natural number. Solved.
arcsin(nk-1) ?
if n = 0 then k = ∞ and just about any value of x works in this case. however x = arcsin(nk -1) still doesn’t work since 0 * ∞ is not defined. so i think the B grade is fair.
(this is all assuming we’re working on the riemann sphere)
x = arcsin(nk-1) + z(2*pi), such that z is any integer.
It's called a literal equation. The problem doesn't state which variable to solve for, but the assumption here is that it is x. Solving literal equations is a basic part of mathematics courses.
I'm a mathematician and I can't recall a time I've ever heard the term "literal equation." When I was in grade school the instructions were always "solve for x" if x was the variable being solved for.
Maybe it's not universal but in school literal equation basically meant there were letters instead of numbers.
It's the term we use for instance when going from the equation of a line like y=3x+2 to lines in general y=ax+b (a and b in ℝ)
And i agree it's a lot better to specify to solve for x (because you can solve for anything or have multiple variables).
Although x being a variable, and solving for it would be the most logical assumption.
I teach secondary and postsecondary math courses. The term "literal equation" was used in Texas where I taught for 17 years. The Algebra 1 state standard A.12E says that students are expected to "solve mathematic and scientific formulas, and other literal equations, for a specified variable." I also taught college undergrad courses in Texas, including College Algebra, and I don't recall ever seeing the the term used there, but I used it in class because my students were familiar with it. Now I teach in Oregon, and the term is not a part of this state's standards from what I can tell.