this post was submitted on 22 Jan 2024
115 points (100.0% liked)
Math Memes
1070 readers
1 users here now
Memes related to mathematics.
Rules:
1: Memes must be related to mathematics in some way.
2: No bigotry of any kind.
founded 1 year ago
MODERATORS
you are viewing a single comment's thread
view the rest of the comments
view the rest of the comments
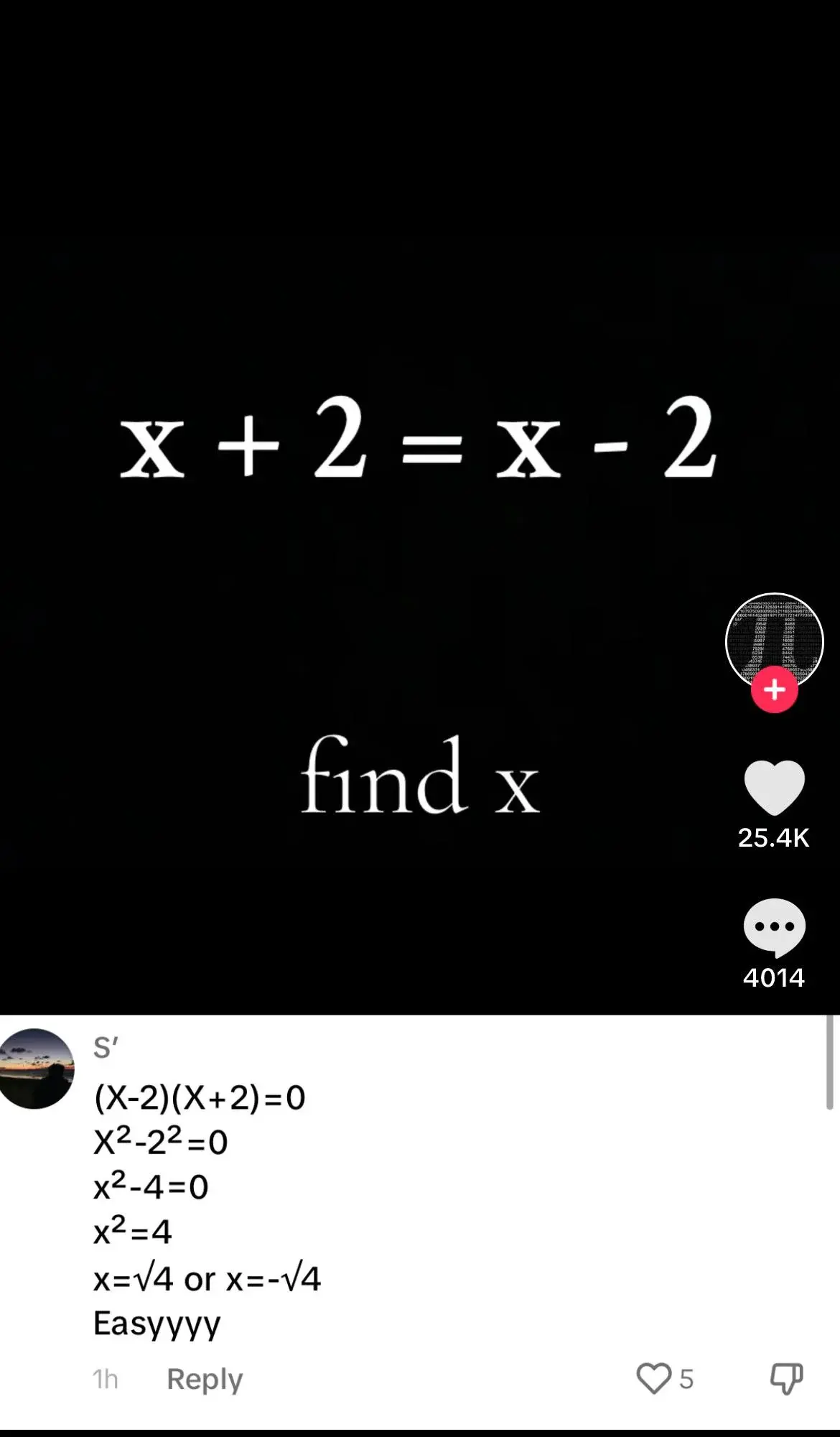
Can someone smart explain it to dumb me
Explanation: How did they get from
x + 2 = x - 2
to
(x+2)(x-2)=0?
That's not a valid step.
To further clarify,
(x+2)(x-2) means to take the result of X+2 and times it with the result of x-2.
While it is common in algebra to bring the other side over, in order to simplify it, this isn't how you'd do it.
Here, you'd either cancel out the X (by removing it on both sides) or the -2 (by adding 2 to both sides) over to make 2=-2 or X+4=X respectively, which are both nonsense equations.
and multiply it with the result
Both are correct.
Not really, no… “times” is not a verb. You can multiply 2 by 2, and you can express that as “2 times 2”, but it is not correct to “times 2 by 2”.
...seems to be pretty correct to me:
https://www.wordreference.com/es/translation.asp?tranword=multiplying
Not sure what you think the relevance of a Spanish-English translation of the word “multiplying” has here… but nonetheless, you can see the correct usage of the word “multiply” versus the word “times” in my explanation above. For further clarification I would suggest a real dictionary, like Oxford, Meriam-Webster, etc.
I’m sure plenty of people will continue to make the mistake and it will become an accepted variant, though I wouldn’t consider it to be the correct usage of the word. Similar to the word “irregardless”, it’s a word, it’s used incorrectly in place of “regardless” very often, and therefore is an accepted variant. It’s just not the correct word to use. This is why I offered you my initial correction.
It's a more authoritative answer than a random comment by a grammar nazi.
Also the dictionaries you mentioned aren't great about including common informal language, which is what 'times by' is.
Yes I’m sure those at Oxford and MW could learn a thing or two from wordreference.com’s Spanish translation, which made the same mistake you did.
Thanks for calling me a nazi though, during otherwise polite conversation… have a good one.
I called you a grammar nazi because it's a perfect description of your behaviour in this conversation, right down to a need to be the only one who's right and being unable to tolerate colloquialisms.
https://en.m.wiktionary.org/wiki/grammar_Nazi
https://www.dictionary.com/e/pop-culture/grammar-nazi/
For a grammar nazi you sure don't seem to read all that carefully.
they start off with S' though... looks like they pretended to try to derive?
I thought that was their profile name
oh fuck me, you seem to be correct
Almost everything is wrong in his answer.
The correct answer is, it's unsolvable.
X + 2 = X - 2
X - X = - 2 - 2
0 = - 4
The real correct answer is that it only works mod 4
Only the first step is wrong.
Yeah, my bad 👍.
multiply both sides by 0, add x. x=x
It’s not solvable using traditional algebra.
Typically you would try to get all of the variables on one side, and all of the numbers on the other.
So in this instance, you’d start by moving them around to get things together:
x+2 = x-2
x+2-x = -2
x-x = -2-2
But then you simplify, and cancel out any variables that need to be cancelled. In this case we see “x-x” so that cancels out to 0. And we see -2-2 which simplifies into -4. So the end result is:
Which is obviously a nonsense answer. In the original post, homeslice did the first step wrong, moved everything over to the left incorrectly, (inadvertently setting the whole equation equal to 0) and the whole thing was downhill from there; Since the first step of their solution was wrong, everything behind it was also wrong.
You know how you sometimes make a mistake in one line, but after doing a few lines, you go back to actually writing the equation correctly? Happened to me all the time in uni. It's basically because you were thinking of doing the next line or whatever, and you just forgot that a var or const was somewhere in there, or you just didn't copy (or copy it correctly) in the next line, but the memory of that var/const remained in your brain, so after doing a few lines, the equation is now simple enough so your brain knows something should be there, but it's missing. Sure, we almost always caught up with the mistake, go back, correct the last few lines and carry on. But, every once in a while, you don't, and you carry on solving the equation, and you get a correct solution, but from a purely mathematical standpoint, yes, that solution is not correct.
My math proffesor in uni had an interesting take on this. He said, you didn't do 1 mistake and then correct it to get the right answer, but you actually made 2... which is worse... according to him. And I have to say, at that time, I didn't agree, but let's be honest... he is correct. So, he went a lot harder on those students that did this type of mistake than the ones that just made 1 and carried on solving the equation like nothing happened.
nah... its still just one error: that of transcribing your process.
it's like a cosmic ray randomly changed a digit in the memory cells that hold the stringbuffer prepared to be printed.
and then the computation carries on with the internal representation of the whole process still with correct data.
i understand your profs pov though
From an engineering standpoint, I don't agree with him. We make errors all the time, it's basically how we learn how to do things the right way (try, fail, repeat). Not to mention rounding errors, we also make GIGANTIC ones (not all the time, but still).
But, he's a mathematician, not an engineer. So, as I said, from a purely mathematical standpoint, yes, he is correct.
well, yeah... xD as i said, i understand that pov. if that printout WAS the process, then yes.
and for an alien that only receives that printout milled into a goldbar attached to a satellite: that would be a bummer ;3
There isn't a valid answer to the question.
Ignore the numbers, and just think about this:
Is there a number that you can add 2 to, that would equal the same about as if you subtracted 2 from it?
The answer is no.
So the person, who is pretending to be smart, just did a bunch of fake math.
Also √4 = 2, so the "answer" they have is just them trying to re-write the question x + 2 = x - 2.
√4=+-2
The square root of x is usually defined as the positive real number that squares to x, so x^2 = 4 => x = +-2 but sqrt(4) = 2, not +-2
The complex sqrt function is multivalued, but that opens a whole other can of worms
And even if you allowed sqrt(4) = ±2, it would still be invalid to evaluate it to -2 on one side of the equation, but then use +2 on the other side.
Of course, you can only choose one at a time, not mix and match, lol 😂.
Oh yeah, you're right, now I remembered 🤦. Been a while 😂, almost 20 years.