this post was submitted on 04 Aug 2024
237 points (98.8% liked)
memes
22757 readers
480 users here now
dank memes
Rules:
-
All posts must be memes and follow a general meme setup.
-
No unedited webcomics.
-
Someone saying something funny or cringe on twitter/tumblr/reddit/etc. is not a meme. Post that stuff in !the_dunk_tank@www.hexbear.net, it's a great comm.
-
Va*sh posting is haram and will be removed.
-
Follow the code of conduct.
-
Tag OC at the end of your title and we'll probably pin it for a while if we see it.
-
Recent reposts might be removed.
-
No anti-natalism memes. See: Eco-fascism Primer
founded 4 years ago
MODERATORS
you are viewing a single comment's thread
view the rest of the comments
view the rest of the comments
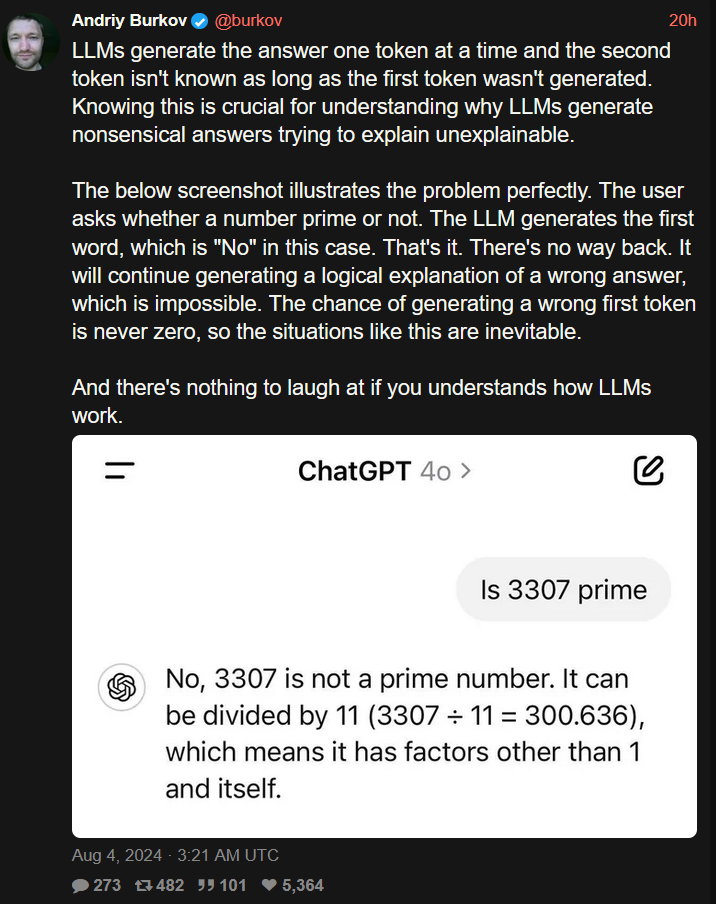
This is also why they create tons of confirmation bias
Like if this prompt was “tell me why 3307 is a prime number” it would probably be correct.
It would be, but thats because you already told it the answer to the original question.
Assuming you don't know if 3307 is prime, if you ask it like this for any number it wil (almost) always say the number is prime.
Edit: I did the inverse with 3307 and it was doing so good but then completely fumbled at the end lmao
So far so good
Uhh ok I guess.
...right
WTF